Asymptotic Expansion of Error Functions

/ Alexander

Define the error function on the whole complex plane by:

\begin{aligned}\mathrm{erf}(z)=\frac{2}{\sqrt{\pi}}\int_{\Gamma}e^{-t^2}dt\end{aligned}

where the path \Gamma is the line segment connecting 0 and z. Error function is a holomorphic function on \mathbb{CP}^1\setminus\{\infty\}, with an essential singularity at z=\infty, now, it is natural to ask what is its asymptotic behavior near the singularity?

To do the evaluation, by Cauchy’s integral theorem, we can write this integral as

\begin{aligned}\mathrm{erf}(z)=\frac{2}{\sqrt{\pi}}\int_0^{|z|}e^{-t^2}+\frac{2}{\sqrt{\pi}}\int_{C}e^{-t^2}dt\end{aligned}

where C is an arc coming from the circle centered at the origin with radius |z|, traveling from |z| to z, see the following figure :

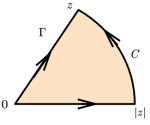
Now, the first term in the RHS is the real error function, which tends to 1 as z goes to \infty, we will focus on the second term in RHS.

By integration by parts:

\begin{aligned}\int_C e^{-t^2}dt&=\int_C\frac{-1}{2t}d\left(e^{-t^2}\right)\\&=\left[\frac{-e^{-t^2}}{2t}\right]_C-\int_C\frac{e^{-t^2}}{2t^2}dt\\&=-\frac{e^{-z^2}}{2z}+\frac{e^{-|z|^2}}{2|z|}-\int_C\frac{-1}{4t^3}d\left(e^{-t^2}\right)\\&=\cdots\\&=e^{-z^2}\left(-\frac{1}{2z}+\frac{1}{4t^3}+\cdots\right)+e^{-|z|^2}\left(\frac{1}{2|z|}+\cdots\right)\end{aligned}

By doing this process over and over again, we will obtain a power series in terms of 1/z. Indeed, we need to check whether the redundant term tends to zero.

The module of the redundant term is

\begin{aligned}\left|\int_C\frac{e^{-t^2}}{2^{N-1}t^N}dt\right|&\leqslant\int_C\left|\frac{e^{-t^2}}{2^{N-1}t^N}\right|dt\\&=\frac{1}{2^{N-1}|z|^N}\int_C e^{-\mathrm{Re}t^2}dt\\&\leqslant \frac{\ell(C)}{2^{N-1}|z|^N}\cdot\mathrm{sup}_{t\in C}\left|e^{-t^2}\right|\\&=\frac{\mathrm{Arg}(z)}{2^{N-1}|z|^{N-1}}\cdot e^{-|z|^2}\longrightarrow 0\end{aligned}

hence which indeed tends to zero as N goes to infinity. Now, to sum up, we have an asymptotic expansion of \mathrm{erf}(z) at z=\infty:

\begin{aligned}\mathrm{erf}(z)=\mathrm{erf}(|z|)+\frac{2}{\sqrt{\pi}}e^{-z^2}\left(-\frac{1}{2z}+\frac{1}{4z^3}+O\left(\frac{1}{z^5}\right)\right)+o(1)\end{aligned}

留下评论