Some Computations on Lie Groups

/ Alexander

The style of this blog is pretty Cartan-ian

Recently, I’m interested in a series paper of Антон Юрьевич Алексеев, they were about the G-valued moment maps. They are Lie Group Valued Moment Maps and Duistmaat-Heckmen Measures and Moduli Space of Flat Bundles Over Surfaces. I was interested in the quasi-Hamiltonian reduction at first, since it is a quite different way from symplectic reduction to construct symplectic structure on the moduli space of flat connections, but then I found the generalized Duistmaat-Heckmen formula on a quasi-Hamiltonian space is rather interesting (it can compute the volume of a moduli space!). To be honest, I was shocked by the frequency of using differential geometry on Lie groups of Антон. In this blog, I will show some detailed computations of the differential geometry on Lie groups (that’s what makes this blog Cartanian).

Now, let G be a Lie group, with the identity element 1, the multiplication is denoted by \cdot, let \mathfrak{g} be its Lie algebra, \exp: \mathfrak{g}\longrightarrow G is expressed for the exponential map on G. We assume g\in G, and X\in\mathfrak{g}. G can act on itself in three canonical ways:

  • The left action: L_g:G\longrightarrow G, h\mapsto g\cdot h, the fundamental vector field of this action is denoted by \underline{X}_L. The tangent map (dL_{g^{-1}})_g of L_{g^{-1}} at g determines a linear map T_gG\longrightarrow\mathfrak{g} (it is a \mathfrak{g}-valued 1-form), it is called the left Cartan-Maurer form on G, denoted by \theta_g.
  • The Right action: R_g:G\longrightarrow G, h\mapsto h\cdot g^{-1}, the fundamental vector field associate to this cation is denoted by \underline{X}_R. The tangent map (dR_g)_g of R_g at g defines a linear map T_gG\longrightarrow \mathfrak{g}, it is called right Maurer-Cartan form, denoted by \bar{\theta}_g.
  • The Adjoint action: \mathrm{ad}_g:G\longrightarrow G, h\mapsto ghg^{-1}, the fundamental vector field associate to this action is denoted by \underline{X}_{A}. Its differential at 1 is called the adjoint action on \mathfrak{g}, denoted by \mathrm{Ad}_g=(d\mathrm{ad}_g)_1:\mathfrak{g}\longrightarrow\mathfrak{g}.

If we choose an adjoint invariant inner product on \mathfrak{g}, namely \langle\cdot,\cdot\rangle_{\mathfrak{g}}, we can define a canonical Cartan 3-form:

\begin{aligned}\chi:=\frac{1}{4}\langle \theta,[\theta,\theta]\rangle=\frac{1}{4}\left\langle\bar{\theta}, \left[\bar{\theta},\bar{\theta}\right]\right\rangle\end{aligned}

where [\theta,\theta]=2\theta\wedge\theta. (Anton used \frac{1}{12} as the coefficient of the Cartan 3-form, but I think \frac{1}{4} could agree with the most results.)

The Maurer Cartan forms will satisfy the Maurer-Cartan equation:

Theorem 1 (Maurer-Cartan Equation): We have the following equations:

d\theta+\theta\wedge\theta=0,\quad d\bar{\theta}-\bar{\theta}\wedge\bar{\theta}=0

The proof can be found in many (or only a few) differential geometry textbooks (not textbooks of Lie theory), such as Spivak’s Differential Geometry and Koboyashi’s.

Theorem 2: We have the following relations:

\bar{\theta}_g=\mathrm{Ad}_g\theta_g,\qquad \theta_g=\mathrm{Ad}_{g^{-1}}\bar{\theta}_g

proof. We have following commutative diagram:

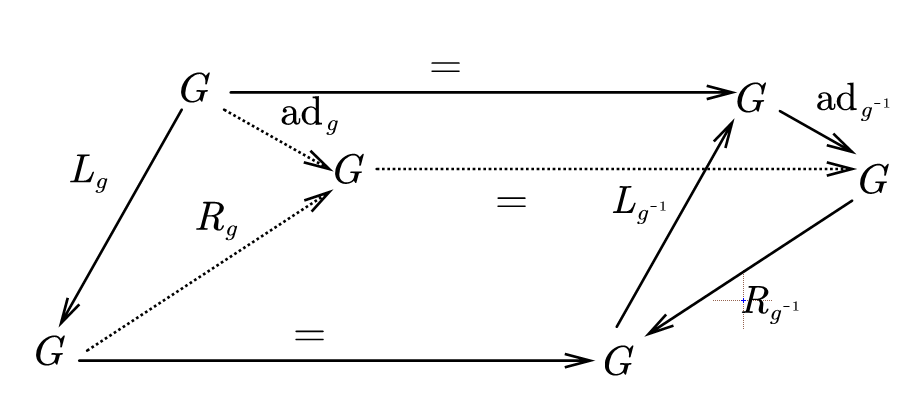
by differentiating this diagram, we have:

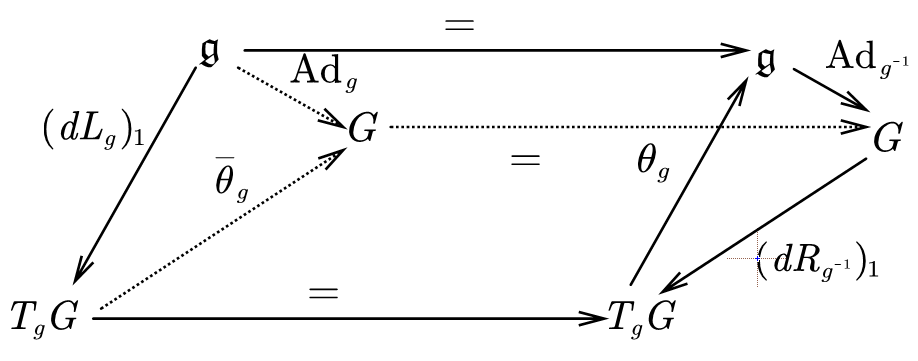
Hence the relations are illustrated in this commutative diagram. \blacksquare

Next, we shall investigate the fundamental vector fields of those three canonical actions:

Theorem 3: We have

\theta_g\underline{X}_L(g)=\mathrm{Ad}_{g^{-1}}X,\quad \bar{\theta}_g\underline{X}_R(g)=-\mathrm{Ad}_{g}X

and for adjoint action, we have

\underline{X}_A(g)=\underline{X}_L+\underline{X}_R.

hence consequently, by Theorem 2, we have

X=\bar{\theta}\underline{X}_L=-\theta\underline{X}_R

proof. By definition, we have

\begin{aligned}\theta_g\underline{X}_L(g)&=\theta_g\left(\left.\frac{d}{dt}\right|_{t=0}(\exp tX)g\right)\\&=\left.\frac{d}{dt}\right|_{t=0}g^{-1}(\exp tX)g=\mathrm{Ad}_{g^{-1}}X\end{aligned}

Similarly, for right action we have:

\begin{aligned}\bar{\theta}_g\underline{X}_R(g)=\left.\frac{d}{dt}\right|_{t=0}g(\exp -tX)g^{-1}=-\mathrm{Ad}_gX\end{aligned}

Now , for adjoint action, we have

\begin{aligned}\theta_g\underline{X}_A(g)&=\left.\frac{d}{dt}\right|_{t=0}\left(g^{-1}(\exp tX)g\right)\exp(-tX)\\&=\theta_g\underline{X}_L-X=\mathrm{Ad}_{g^{-1}}X-X\end{aligned}

hence

\begin{aligned}\underline{X}_A(g)&=\theta_g^{-1}\mathrm{Ad}_{g^{-1}}X-\theta_g^{-1}X\\&=\underline{X}_L(g)-\bar{\theta}_g^{-1}\mathrm{Ad}_gX\\&=\underline{X}_L(g)+\underline{X}_R(g)\end{aligned}

As was to be shown. \blacksquare

Remark: In some contents, the fundamental vector field is defined by taking \exp(-tX), so that \underline{\cdot}: \mathfrak{g}\longrightarrow \mathfrak{X}(M) is a Lie algebra homomorphism, if we omit that minus, it is an anti-homomorphism.

Theorem 4: Define the multiplication map \mu_1:G\times G\longrightarrow G, \mu_1(a,b)=a\cdot b, then we have

\mu_1^*\theta_{ab}=\mathrm{Ad}_{b^{-1}}\pi_1^*\theta_a+\pi_2^*\theta_b

here \pi_1,\pi_2 are the projection of G\times G onto the 1st and the 2nd component respectively. And consequently, by Theorem 3, we have for right Maurer-Cartan form:

\mu_1^*\bar{\theta}_{ab}=\pi_1^*\bar{\theta}_a+\mathrm{Ad}_a\pi_2^*\bar{\theta}_b

proof. For any V=(V_1,V_2)\in T_{(a,b)}(G\times G)=T_aG\times T_bG, we have, by definition

\mu_1^*\theta_{ab}V=\theta_{ab}(d\mu_1)_{(a,b)}(V_1,V_2)

Notice that, the curve

\gamma_1(t)=a\cdot \exp t\theta_aV_1: \mathbb{R}\longrightarrow G

satisfies the initial condition \gamma_1(0)=a, \gamma_1'(0)=V_1, indeed:

\begin{aligned}\gamma_1'(0)&=\left.\frac{d}{dt}\right|_{t=0}a\cdot\exp t\theta_aV_1=\underline{-\theta_aV_1}_R(a)\\&=-\bar{\theta}_a^{-1}\mathrm{Ad}_a\theta_aV_1=\bar{\theta}_a^{-1}\bar{\theta}_aV_1\\&=V_1\end{aligned}

hence the same thing holds for \gamma_2(t)=b\exp t\theta_bV_2, hence by definition:

\begin{aligned}\theta_{ab}(d\mu_1)_{(a,b)}(V_1,V_2)&=\left.\frac{d}{dt}\right|_{t=0}b^{-1}a^{-1}(a\exp t\theta_aV_1)\cdot(b\exp t\theta_b V_2)\\&=\left.\frac{d}{dt}\right|_{t=0}\left(b^{-1}(\exp t\theta_aV_1)b\right)\cdot(\exp t\theta_bV_2)\\&=\mathrm{Ad}_{b^{-1}}\theta_a(d\pi_1)_{(a,b)}V+\theta_b(d\pi)_{(a,b)}V\end{aligned}

hence \mu_1^*\bar{\theta}_{ab}=\pi_1^*\bar{\theta}_a+\mathrm{Ad}_a\pi_2^*\bar{\theta}_b, as was to be shown. \blacksquare

Corollary 4-1: If we define \mu_2(a,b)=a^{-1}b^{-1}, then we have

\mu_2^*\bar{\theta}_{a^{-1}b^{-1}}=-\mathrm{Ad}_{a^{-1}}\pi_2^*\theta_b-\pi_1^*\theta_a

\mu_2^*\theta_{a^{-1}b^{-1}}=-\mathrm{Ad}_b\pi_1^*\bar{\theta}_a-\pi_2^*\bar{\theta}_b

Theorem 5: Let M be a manifold, endowed with an G-action, there 2 G-equivariant maps \mu_1,\mu_2: M\longrightarrow G, where G is endowed with its own adjoint action, then we have

(\mu_1\cdot\mu_2)^*\theta=\mathrm{Ad}_{\mu_2^{-1}}\mu_1^*\theta _{\mu_1}+\mu_2^*\theta_{\mu_2}

proof. For V\in T_xM, extend it to a smooth vector field, still denoted by V, the trajectory passing through x\in M will be denoted by \gamma_V(t), it satisfies the initial condition \gamma_V(0)=x, and \gamma_V'(0)=V.

By definition, we can compute by Leibniz rule:

\begin{aligned}(\mu_1\cdot\mu_2)^*\theta (V)&=\left.\frac{d}{dt}\right|_{t=0}\mu_2^{-1}(x)\mu^{-1}_1(x)\mu_1(\gamma_V(t))\mu_2(\gamma_V(t))\\&=\left.\frac{d}{dt}\right|_{t=0}\left[\mu_2^{-1}(x)\mu^{-1}_1(x)\mu_1(\gamma_V(t))\mu_2(x)\right]\cdot\left[\mu_2^{-1}(x)\mu_2(\gamma_V(t))\right]\\&=\mathrm{Ad}_{\mu_2^{-1}}\theta_{\mu_1}(d\mu_1)_xV+\theta_{\mu_2}(d\mu_2)_xV\end{aligned}

this implies the result. \blacksquare

In Anton’s paper, he defined the quasi-Hamiltonian space (M, G, \mu, \omega), which consists of following data:

  • A smooth manifold M, together with a 2-form \omega;
  • A G-action on M, together with a group-valued moment map \mu:M\longrightarrow G, which is equivariant, where G is endowed with its adjoint action, i.e, the following diagram commutes:

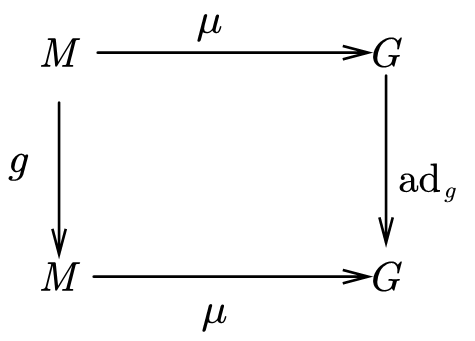
The moment map, and the 2-form \omega should satisfy the following properties

  • \begin{aligned}\iota_{\underline{X}}\omega=\frac{1}{2}\mu^*\langle\theta+\bar{\theta},X\rangle\end{aligned}, for all X\in\mathfrak{g}
  • d\omega=-\mu^*\chi
  • \ker \omega_x=\{\underline{X}(x)|\mathrm{Ad}_{\mu(x)}X+X=0\}, for all x\in M

I will explain why we request these 3 properties. The 1st equation is a natural replacement (I did not see why it is natural) of the usual moment map condition: \iota_{\underline{X}}\omega=-d\mu_X, whre \mu_X(x)=(\mu(x),X), the \mu:M\longrightarrow \mathfrak{g}^* is usual momentum, (,.,) is denoted for pairing.

The 2nd equation, is requesting \omega is G-invariant. For simplicity, we assume our Lie group is connected, hence the 2-form is invariant if and only if \mathcal{L}_{\underline{X}}\omega=0, in Hamiltonian action, it is automatically held since the symplectic form is closed, but in quasi-Hamiltonian case, it is not, since by Cartan magic formula:

\begin{aligned}\mathcal{L}_{\underline{X}}\omega&=d(\iota_{\underline{X}}\omega)+\iota{\underline{X}}d\omega\\&=\frac{1}{2}d\mu^*\langle\theta+\bar{\theta}, X\rangle+\iota_{\underline{X}}d\omega\end{aligned}

In order to compute the 1st assertion, we need the following fact:

Theorem 6: For equivariant \mu, we have

(d\mu)_x\underline{X}(x)=\underline{X}_A(\mu(x))

proof. Notice that the curve \gamma(t)=(\exp tX)x, the trajectory of \underline{X} passing through x. By definition, we have

\begin{aligned}(d\mu)_x\underline{X}(x)&=\left.\frac{d}{dt}\right|_{t=0}\mu(\exp tX)x\\&=\left.\frac{d}{dt}\right|_{t=0}\mathrm{ad}_{\exp tX}\mu(x)\\&=\underline{X}_A(\mu(x))\end{aligned}

as was to be shown. \blacksquare

Next, we shall find what is \frac{1}{2}d\mu^*\langle\theta+\bar{\theta},X\rangle:

\begin{aligned}\frac{1}{2}d\mu^*\langle\theta+\bar{\theta},X\rangle&=\frac{1}{2}\mu^*\langle d\theta+d\bar{\theta}, X\rangle\\&=-\frac{1}{4}\mu^*\langle[\theta,\theta],X\rangle+\frac{1}{4}\mu^*\left\langle\left[\bar{\theta},\bar{\theta}\right],X\right\rangle\\&=\frac{1}{4}\mu^*\langle[\theta,\theta], \theta \underline{X}_R\rangle+\frac{1}{4}\mu^*\left\langle\left[\bar{\theta},\bar{\theta}\right],\bar{\theta}\underline{X}_L\right\rangle\\&=\mu^*\iota_{\underline{X}_L}\chi+\mu^*\iota_{\underline{X}_R}\chi=\mu^*\iota_{\underline{X}_A}\chi\\&=\iota_{\underline{X}}\mu^*\chi\end{aligned}

So, we can see that the \omega is G-invariant, if and only if \iota_{\underline{X}}(d\omega+\mu^*\chi)=0 for all X\in \mathfrak{g}, that is the 2nd equation.

The 3rd condition is requesting that \omega is “as non-degenerate as possible”, since for every X\in\mathfrak{g} satisfying \mathrm{Ad}_{\mu(x)}X-X=0, the contraction \iota_{\underline{X}}\omega is identically zero.

Theorem 4 and Theorem 5 are saying that the double G\times G, endowed with the diagonal adjoint cation of G, with the 2-form defined as follows:

\begin{aligned}\omega_{G\times G}=\frac{1}{2}\left\langle\pi_1^*\theta,\pi_2^*\bar{\theta}\right\rangle+\frac{1}{2}\left\langle\pi_1^*\bar{\theta},\pi_2^*\theta\right\rangle+\frac{1}{2}\left\langle\mu_1^*\theta,\mu_2^*\bar{\theta}\right\rangle\end{aligned}

is a quasi-Hamiltonian space with the commutator as the moment map

\mu=\mu_1\cdot\mu_2:G\times G\longrightarrow G, \,\, (a,b)\mapsto [a,b]=aba^{-1}b^{-1}

留下评论